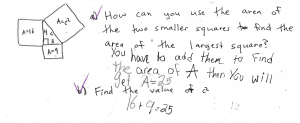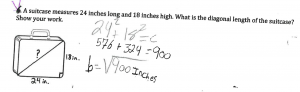December

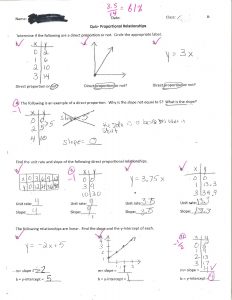
Quiz on Proportional Relationships

 

This student did a better job than most identifying unit rate/slope and y-intercept on the first page of the quiz. However, on the second page, he didn’t do any actual calculations of unit rate. Instead, he just looked at the two different functions and incorrectly reasoned from there. Many of my students filled out the second page of the quiz in a similar fashion. This led me to realize that while they could identify the unit rate when there was an x-value of 1, an equation, or a table that shows a simple multiplication pattern with whole numbers, they didn’t fully understand that the unit rate comes from dividing the y-values by the x-values. They had not internalized this fundamental skill from our previous lessons.

February

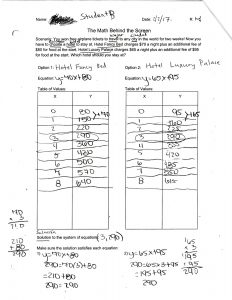
Systems Commercial Project

 

Student B’s work showed a clear understanding of the relationship between a real-world scenario, a linear equation, a table of values, and the solution to a system of equations. Student C and D’s work included a few minor calculation errors that were corrected later in the project, but their work still demonstrated an overall understanding the aforementioned relationships.

In this group’s presentations, the students did a great job using their mathematical evidence (tables and graphs) to explain their choice of which YouTube star to sponsor:

March

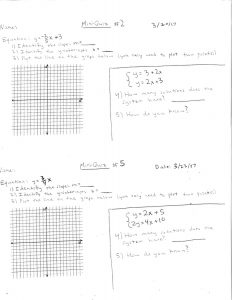
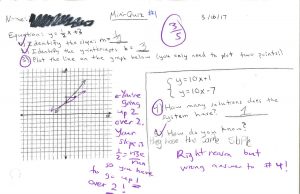
Learning to Master Graphing Linear Equations

 

Here are samples of two of the five mini-quizzes I gave my students, along with one student’s performance on the first mini-quiz. On the first two mini-quizzes, this student scored 60%, for he kept struggling to graph the slope with the correct amount of rise and run, even though he was able to identify the correct slope in the first question each time. After seeing my comments and doing some practice problems with me after school, he scored 100% on the last three quizzes. Many of my students experienced similar growth, as seen in the graph and table of student results from March.

April

Square Roots

 

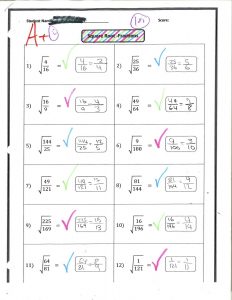
These three worksheets show some of the work my students did to practice and master square roots. During one period, as they “rapid fire” wrote out the square roots of as many perfect squares they could (as seen in the first photo), the classroom was totally silent because they were concentrating so hard. Although I do not believe that a silent classroom in general is a sign of learning, in this case I think it was a testament to my students’ engagement in the material and their pursuit of content mastery. After they had practiced writing all of the square roots on the first worksheet, they used their new knowledge to solve the problems on the subsequent worksheets.

Pythagorean Theorem

After gaining confidence with square roots, students transitioned to the Pythagorean Theorem. Because of the success of the mini-quizzes in promoting skills-based mastery, I gave my students two mini-quizzes during this unit. Here are of six samples of my students’ work on the second mini-quiz, which boasted a class average of 88% (as did the first mini-quiz).

 

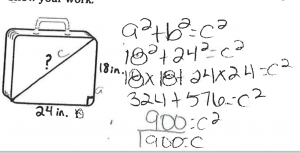
As a summative assessment, I gave my students a longer quiz on the Pythagorean Theorem. Each row below shows student responses from a different question on the quiz. In their responses, students were not only able to recall the formula for the Pythagorean Theorem (row 1), but they were also able to explain why the formula makes sense using the area model (row 2) and then apply it to a real-world scenario (row 3). Throughout the quiz, students supported this conceptual-based mastery with skills-based mastery by successfully computing squares and square roots.