December

After spending a few weeks working with proportional relationships in a variety of real-world scenarios, including the prices of papusas at different restaurants in Worcester and the amount of sugar in different brands and sizes of soda, I gave my students a quiz on the material. The quiz had problems that entailed finding the unit rate/slope from equations, tables, and graphs, as well as a few problems that required a bit more real-world scenario interpretation. My students struggled with both sorts of problems, evidenced by a class average of 66%. Clearly they were not able to transfer their knowledge of either the skill or the concept from previous lessons to the quiz.

February

As we progressed in our study of linear equations, we moved on to working with systems of equations. After having my students explore two real-world scenarios with systems of equations, I noticed that while they understood that the solution to a system of equations was at the intersection of both lines, they didn’t quite understand the mathematical or real-world significance of this. To address both the lack of skill and conceptual understanding, I designed a project in which groups of students analyzed different systems of equations that dealt with real-world business decisions and required them to use their calculations as evidence for their ultimate decision (check out my second round for more details). Through this project, students demonstrated an incredible understanding of the skills (finding the solution using a table and a graph) and the conceptual understanding (how that math informed their business decision). Students of all mathematical and language abilities were able to participate in the project, and I felt that for the first time, my students really understood the connection between the math skills and the overall concept, as well how to use those skills to solve real-world problems.

March

In our next unit, students worked to graph lines using rise/run and equations. Before this unit, they had only graphed linear equations by plotting individual points. Students struggled to master this skill, and I felt that there was a lack of effort on their part to really try and learn it, even after I showed them how much faster it made graphing. After at least two weeks of practice, I gave my students a quiz on the material. Of my 19 students, 14 of them failed it, with many of them earning close to a 0. After reflecting with my program supervisor and supervising practitioner on their disappointing performance, we decided that one of the causes of that performance was that my students did not feel the need for mastery. In previous grades, they had not always been held accountable for really knowing different math skills well, and that attitude towards learning was transferring to my class.

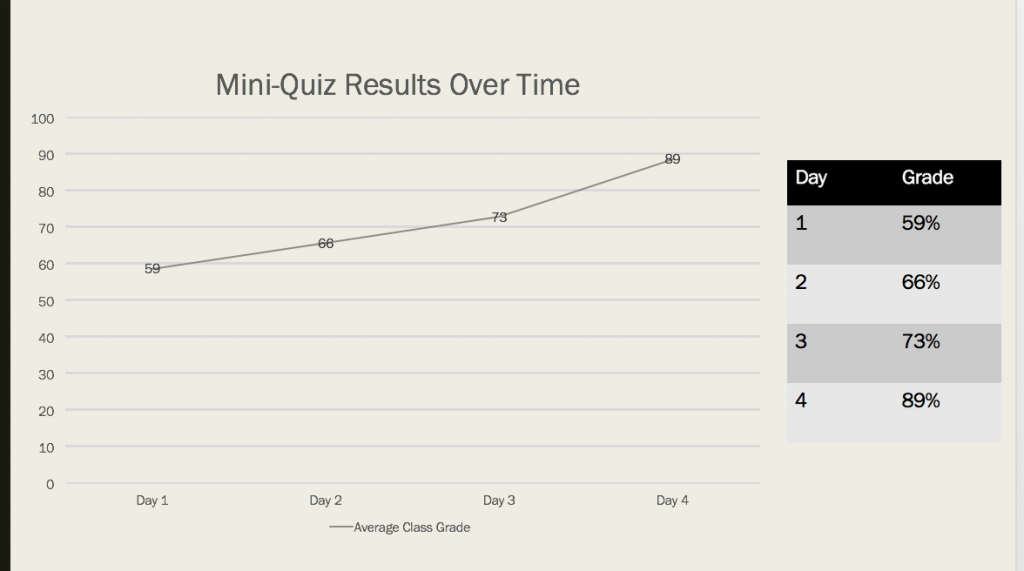
To help my students understand the importance of mastering material, and to allow them to focus just on practicing the skill, I decided to give them a series of mini-quizzes (each composed of five quick questions) on graphing linear equations – one every day for a week. I also provided extra support before school and after school, as well as study guides, which many students took advantage of. As a class, we set the goal of getting to a class average of 80% (4 out of 5 questions correct) by the last quiz. These were the quiz averages from the first four days:

After a steady 7% increase over the first three days, the scores shot up by 16% and exceeded our goal by 9% on the fourth day! My students visibly were excited about their improvement and told me that they felt much more comfortable with the material. I ended up making the fifth quiz optional for those who wanted to raise their individual averages. I count this as huge growth in my students’ learning because they really pushed themselves to master a skill for one of the first times in my class, instead of accepting mediocrity. I think that because of that, they saw themselves as capable learners, which was powerful.

April

We rode this wave of confidence into our square roots and Pythagorean Theorem unit, emphasizing the skill of squaring numbers and finding square roots before conceptually exploring the Pythagorean Theorem, which was the opposite order of how I usually structured units. My students quickly grasped the idea of square numbers and finding square roots, and they eagerly worked through different skills exercises to master that content. 

During the Pythagorean Theorem unit, I gave two mini-quizzes and a longer quiz at the end. On the first mini-quiz, which tested students’ ability to find the length of the hypotenuse, the class averaged 88%. On the second mini-quiz, which tested students’ ability to find the length of a leg of a right triangle, the class averaged 88% again. Again, this success showed that my students were taking their learning of skills-based content seriously.

Unfortunately, because of time constraints, we did not get to solve the real-world Pythagorean problems we had looked at at the start of the unit. However, on their quiz, students had to find the diagonal length of a suitcase given the length and width. Essentially, they had to use the Pythagorean Theorem to find the hypotenuse. 12 out of 16 students (75% of the class) were able to successfully transfer their understanding of the Pythagorean Theorem to this real-world context. On another problem on the quiz, 13 out of 16 students (roughly 81% of the class) were able to accurately explain the conceptual understanding of the Pythagorean Theorem – that the areas of the two smaller squares add to equal the area of the larger square – and then use their knowledge of square numbers and square roots to find the larger area and the length of the hypotenuse.